平面グラフアルゴリズム
お待たせいたしました。Competitive Programming Advent Calendar 2019 8日目の記事です。
平面グラフとは
平面グラフとは、平面に辺を交差させずに描画できるグラフのことをいいます。現実世界の例では多くのroad mapがそうであったりします。平面グラフでは、たとえば最短路問題がで解けたり(Frederikson)、多くの最適化問題で、通常のグラフよりも効率的なアルゴリズムが発見されています。
この記事では平面グラフの性質や、アルゴリズムなどを紹介していこうと思います。もともとは実装しようと思っていたんですが、ちょっと人生が忙しいので保留です(一生保留しそう)(ごめんなさい)。
基本編
Eulerの公式
連結な平面グラフについて、頂点数を
, 辺数を
, 面数を
とすると
が成り立つ。非本質ですが、頂点は0次元、辺は1次元、面は2次元なので、符号と
が共通していますね。暗記向けです。
単純な平面グラフ(
)について、
これにより、辺の数がであることがわかります。そうすると面の数も
です。平面グラフアルゴリズムの計算量に
しか現れないのはこのためです。ちなみに、アルゴリズムの計算量などで
といっても定数倍が大きいものが多い印象です。
Kuratowskiの定理
グラフが平面グラフである必要十分条件が、「
は
をマイナーに含まない」ことをいう定理です。
は
頂点の完全グラフ、
は
頂点の完全二部グラフを指します。グラフ
がグラフ
のマイナーであるとは、
が
から、(1)辺の除去, (2)辺の縮約, (3)孤立点の除去を繰り返して得られることをいいます。
それぞれと
https://www.researchgate.net/figure/Excluded-minors-for-planar-graphs_fig1_238872253
グラフの集合がある性質
に対してminor-closedであるとは、
の要素を縮約したグラフも性質
を満たすことをいいます。明らかに、「平面に描画できているグラフを縮約したグラフは平面に描画できる」ので、平面グラフはminor-closedなグラフの集合となります。興味深い点は、
はいずれも平面に描画できないのですが、平面に描画できる必要十分条件がこの2グラフの(マイナーとしての)有無で決定されるということです。証明は省略しますが、興味のある方はぜひ調べてみてください。
中級編
グラフの平面性判定
与えられたグラフが平面グラフかどうかはで判定ができます。これめっちゃすごいですね。アルゴリズムは、いろいろなものが開発されてきましたが、Boyerのアルゴリズムが有名な気がします。
アルゴリズムの説明(アルゴリズムは全然中級じゃないです)
お絵かきをしました。適当に書いたグラフなのでとくにコーナーケースじゃないです(すみません)
本質は線形にするための実装と正当性の証明なんですが、手でやる分には比較的簡単にできます。
- グラフをdfsし、訪れた順にidを振っていく。dfs木と後退辺を覚えておく
- 各辺の優先度を
とする。つまり両端のidのmin
- 辺を優先度の大きい順に追加していく。同じ優先度はなんでもいいけどdfs木の辺優先
- そのときに2連結になるように、頂点を適宜増やしていく
- 新たなループが生成されるとき、externally activeな頂点を外平面に向けるようにflipする(将来的に処理される辺はすべて外平面に来ているはず)
- 最後まで追加できれば描画完了。無理なら平面グラフでない
ある頂点がexternally activeというのは、その頂点またはその子孫から後退辺をたどって、今見ている優先度よりもidの小さい頂点に行けるということで、要は今後辺を追加されるときに面に埋め込まれちゃうかもしれない、気をつけなければいけない頂点です。
描画完了できない場合は平面グラフではないんですが、詰むケースは数パターンに場合分けされ、それぞれの場合についてどの部分グラフが禁止マイナーになっているかを調べることができます。
かなり雑に説明しちゃったんですが、 http://www.th.cs.meiji.ac.jp/assets/researches/2007/toyota/index.html に日本語記事があるので気になる方は照らし合わせながら追ってみてください。
Separator定理
えー、一番の本質です。平面グラフで一番うれしい性質です。グラフの頂点集合の分割
で、(1)どの辺も
を直接結ばなく、(2)A, Bの頂点重みは全体の2/3以下にできるとき、頂点集合
を
のセパレータと呼びます。グラフに
のセパレータが存在するかはかなり重要な関心であり、なぜかというと、
のセパレータが存在するなら、分割統治アルゴリズムが使えるからです。うれしいことに、平面グラフは
のセパレータをもつことが知られており、
でセパレータを構築できますLipton & Tarjan。実際多くの平面グラフアルゴリズムはこのセパレータの性質によって高速性が導かれています。
木幅が
この記事ではあまり深く書くことがないです。
たぶん上級編
直線による描画
平面グラフの定義において、平面に描画するときに直線を使う必要はありませんが(曲線でよい)、実は任意の平面グラフは直線のみを用いて平面に描画が可能です。もっと言うと、のサイズのグリッド上の格子点に頂点を配置して、かつ、直線のみを使って描画することも可能です。
最大カット
最大カット問題は、一般グラフにおいてNP-Hardであることが知られていますが、平面グラフにはアルゴリズムが存在します
アルゴリズムの説明
これもまたさまざまなアルゴリズムが提案されてきたのですが、シンプルで有名なのがA simple MAX-CUT algorithm for planar graphsだと思います。
平面グラフと双対グラフです。
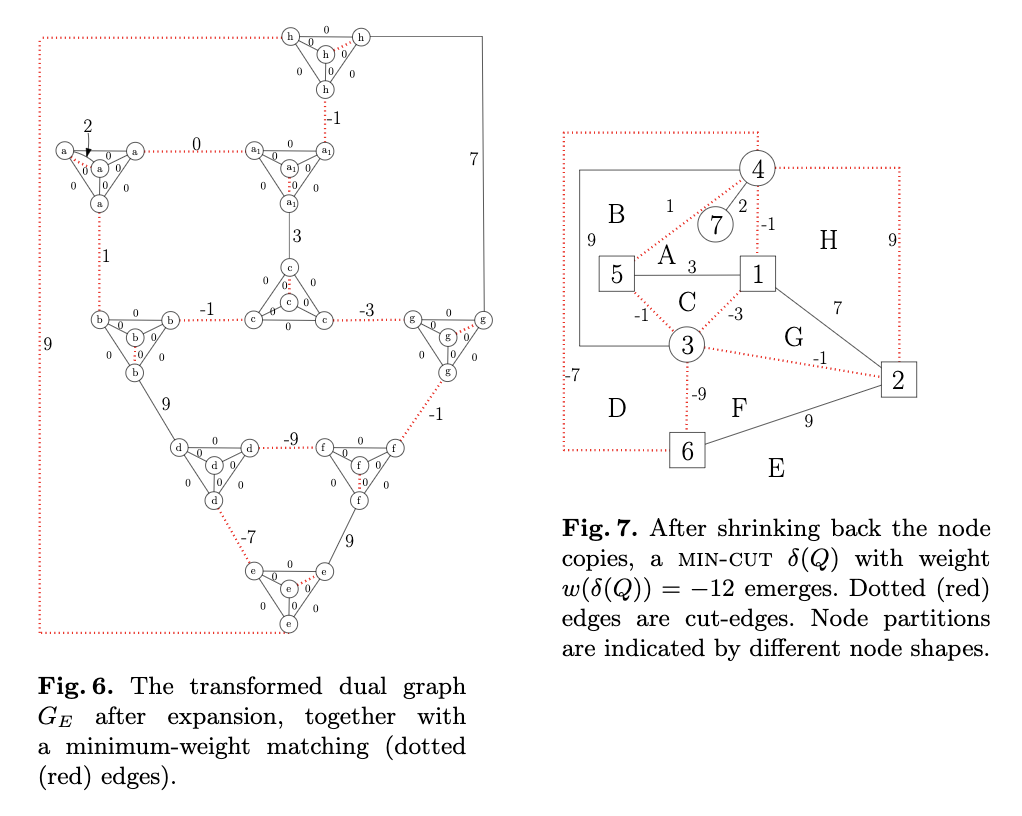頂点をに倍加して、最大マッチングを考えます。
連結な単純グラフ
が入力として与えられたとき、まず
をとる。双対グラフの辺のコストは、その辺が横切る元のグラフの辺のコストと同じにする。
に置き換えたグラフを考える。
以上のグラフでmaximum weighted matchingを考える。必ずperfect matchingが存在することが示せ、このとき、各
双対グラフでのEulerian subgraphと元のグラフのカットには1対1対応があり、この最大重みeulerian subgraphが元のグラフでの最大cutになっている。
計算量についてまとめます。平面グラフの双対グラフも平面グラフであり、頂点数、辺の本数もで、頂点を4倍加してもオーダーは変わりません。あとは平面グラフのmaximum weighted matchingを考えればいいのですが、これはTarjanによると
なので、そのままmax-cutもこのオーダーで解けることになります(クソ雑)。
最小交差数
A separator theorem for minor-closed classesによると、固定されたについて最小交差数が
以下か判定する線形アルゴリズムがあるそうです。
同型判定
平面グラフの同型判定は線形で可能です https://dl.acm.org/citation.cfm?id=803896
Minor-closedグラフとセパレータ
さて、平面グラフはminor-closedなグラフのクラスでしたが、minor-closedな性質をもつぐらふの集合は他にもあります。たとえば、toroidalグラフとよばれる、torusに辺の交差なしに埋め込めるグラフもminor-closedです。
A Separator Theorem in Minor-Closed Classesでは、minor-closedなグラフはのセパレータをもつのでは？という話がされていて、実際に
をマイナーとして含まないグラフについて
のセパレータを持つことを証明しています。これは応用範囲が広く、たとえばbounded degreeのグラフが
のセパレータをもつことなどがすぐに導かれます。
ちなみに、bounded average degreeグラフはこの性質を満たしません(証明はErdos)。
のセパレータをもつなら、分割統治が回るので、平面グラフ以外にも多くのminor-closedなグラフについて平面グラフの場合と類似する高速なアルゴリズムがあると思います(あまり詳しくありません)
最後に
平面グラフやべーーーーー やべーーーと話題に
