not-all-equal-3sat系証明のテクニック
グリッドグラフの描画とか、horizontalとverticalしか使っちゃだめ系描画など、一般に「自由度が相対的に制限される」ようなセッティングにおける可能性判定の証明に使える気がする。
証明のテクは、「必ずこの配置しかありえない」ような配置を組み合わせ、これから追加できる要素の配置を一通りに制限する。
not-all-equal-3satのインスタンスを目的のアルゴリズム(NP-Completeであると証明したいもの)を使って解くことを考える。
not-all-equal-3satの本質は、各clauseについて、すべてをtrueにしてはいけないということで、上述したような、配置が固定されるオブジェクトをうまく組み合わせ、個の隙間に要素を敷き詰めるような設定を作る。これで、もし目的のアルゴリズムで敷き詰めが可能かどうか判定できるならnot-all-equal-3satが解けてしまう、という流れにする。
Complexity dichotomy on partial grid recognition
ウ ン チ ー コ ン グ !
グリッドに描画できるグラフのクラスをいろいろ考えて、PolynomialなものとNP-Completeなものに分けた。一般の描画はNP-Complete(そもそも木が無理なので)
次数がの要素のみからなるグラフを
-Graphとよぶことにする。たとえばパスグラフは
-Graphで、サイクルは
-Graphである。

雑感
詰めるところは一応あって
- 三角形グリッドならどうなるか
- 次元上げたときにどうなるか
でもこれやってて楽しいか?という気持ちになった。
この本にめちゃめちゃ乗ってそうだしサーベイ漏れがないかこれでチェックして絵
The Complexity of Minimizing Wire Lengths in VLSI Layouts
タイトル練り直せ
Theorem
最大次数が4の木をグリッドに埋め込めるかはNP-Complete
証明
not-all-equal 3satに帰着する。これは、3CNF式が与えられたときに、各clauseに少なくともひとつfalseになるリテラルが含まれるように充足可能か、という問題。
つまり、3CNF式が与えられたときに、それから最大次数が4の木を構成し、木がグリッドに埋め込める iff not-all-equal 3satの充足が存在する、という感じにしたい。
準備
以下のような木は向きの自由を無視して、一意な埋め込みがあります。また、これをつなげたもの(右)も一意な埋め込みになります。

3SATから木を構成

個の変数が存在するとして、横に
個、上下に長さ
の骨格をつくる。骨格の端は、これから先に追加する枝の方向を確定させるためのもの(必ず横向きになるように)。
ここから、間の列について、clauseからなる制約を付け加えていく。具体的には、
番目のclauseに
が登場しない場合、対応する箇所(下画像参照)に横棒(striker)を一つ足す。

さて、こうして構成されたグラフについて、グリッドに埋め込めるかどうかと、もとのCNF式にnot-all-equal-3sat充足が存在するかが等価になることを示す。
ポイントとしては、間の列に関して、上下を逆にしてもグラフとして同型ということである。また各骨格について、左右反転させたものも同型になるという点が重要である。結果的にある埋め込みが存在したとき、上になっている方をTrue, 下になっている方をFalseとした充足が存在することになる。
さて、各clauseについて、変数は3つある(と
があれば無視できるので、異なる変数が3つ、と考えて良い)ので、各行について、clauseに登場しない変数分として
本のstrikerが存在する。これについて、各変数がもしすべてtrueの場合、3本のstrikerが追加され、
本のstrikerになってしまう。一方、そうでない場合、strikerは
本以下である。
いま、strikerを埋め込める箇所は、free columnと呼ばれる箇所しかない。したがって、もしnot-all-equal-3satが充足可能でない場合、平面埋め込みが存在しない。
逆にnot-all-equal-3satが充足可能である場合、trueのものを上にし、falseのものを下にした場合、上述する性質を満たすような埋め込みが存在する(証明終了)
ウ ン チ ー コ ン グ
一応背景としては、木をmaximum edge length(とは?)を最小化して埋め込みたい、というものがあったっぽい。さすがに追わないと思う。 あと、complete binary treeで一意なうめこみがあるものがあるらしく(31頂点とか。ほかはしらんけどまあ似たような感じでしょ)、その場合についても本定理を拡張できるらしい。しらんけど。
ウ ン チ ー コ ン グ !
Partial Grid
http://www.graphclasses.org/classes/gc_440.html
判定はNP-Completeでした。
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
ウ ン チ ー コ ン グ !
平面グラフアルゴリズム
お待たせいたしました。Competitive Programming Advent Calendar 2019 8日目の記事です。
平面グラフとは
平面グラフとは、平面に辺を交差させずに描画できるグラフのことをいいます。現実世界の例では多くのroad mapがそうであったりします。平面グラフでは、たとえば最短路問題がで解けたり(Frederikson)、多くの最適化問題で、通常のグラフよりも効率的なアルゴリズムが発見されています。
この記事では平面グラフの性質や、アルゴリズムなどを紹介していこうと思います。もともとは実装しようと思っていたんですが、ちょっと人生が忙しいので保留です(一生保留しそう)(ごめんなさい)。
基本編
Eulerの公式
連結な平面グラフについて、頂点数を
, 辺数を
, 面数を
とすると
が成り立つ。非本質ですが、頂点は0次元、辺は1次元、面は2次元なので、符号と
が共通していますね。暗記向けです。
単純な平面グラフ( )について、
)について、
これにより、辺の数がであることがわかります。そうすると面の数も
です。平面グラフアルゴリズムの計算量に
しか現れないのはこのためです。ちなみに、アルゴリズムの計算量などで
といっても定数倍が大きいものが多い印象です。
Kuratowskiの定理
グラフが平面グラフである必要十分条件が、「
は
をマイナーに含まない」ことをいう定理です。
は
頂点の完全グラフ、
は
頂点の完全二部グラフを指します。グラフ
がグラフ
のマイナーであるとは、
が
から、(1)辺の除去, (2)辺の縮約, (3)孤立点の除去を繰り返して得られることをいいます。

それぞれと
https://www.researchgate.net/figure/Excluded-minors-for-planar-graphs_fig1_238872253
グラフの集合がある性質
に対してminor-closedであるとは、
の要素を縮約したグラフも性質
を満たすことをいいます。明らかに、「平面に描画できているグラフを縮約したグラフは平面に描画できる」ので、平面グラフはminor-closedなグラフの集合となります。興味深い点は、
はいずれも平面に描画できないのですが、平面に描画できる必要十分条件がこの2グラフの(マイナーとしての)有無で決定されるということです。証明は省略しますが、興味のある方はぜひ調べてみてください。
中級編
グラフの平面性判定
与えられたグラフが平面グラフかどうかはで判定ができます。これめっちゃすごいですね。アルゴリズムは、いろいろなものが開発されてきましたが、Boyerのアルゴリズムが有名な気がします。
アルゴリズムの説明(アルゴリズムは全然中級じゃないです)
お絵かきをしました。適当に書いたグラフなのでとくにコーナーケースじゃないです(すみません)

本質は線形にするための実装と正当性の証明なんですが、手でやる分には比較的簡単にできます。
- グラフをdfsし、訪れた順にidを振っていく。dfs木と後退辺を覚えておく
- 各辺の優先度を
とする。つまり両端のidのmin
- 辺を優先度の大きい順に追加していく。同じ優先度はなんでもいいけどdfs木の辺優先
- そのときに2連結になるように、頂点を適宜増やしていく
- 新たなループが生成されるとき、externally activeな頂点を外平面に向けるようにflipする(将来的に処理される辺はすべて外平面に来ているはず)
- 最後まで追加できれば描画完了。無理なら平面グラフでない
ある頂点がexternally activeというのは、その頂点またはその子孫から後退辺をたどって、今見ている優先度よりもidの小さい頂点に行けるということで、要は今後辺を追加されるときに面に埋め込まれちゃうかもしれない、気をつけなければいけない頂点です。
描画完了できない場合は平面グラフではないんですが、詰むケースは数パターンに場合分けされ、それぞれの場合についてどの部分グラフが禁止マイナーになっているかを調べることができます。
かなり雑に説明しちゃったんですが、 http://www.th.cs.meiji.ac.jp/assets/researches/2007/toyota/index.html に日本語記事があるので気になる方は照らし合わせながら追ってみてください。
Separator定理
えー、一番の本質です。平面グラフで一番うれしい性質です。グラフの頂点集合の分割
で、(1)どの辺も
を直接結ばなく、(2)A, Bの頂点重みは全体の2/3以下にできるとき、頂点集合
を
のセパレータと呼びます。グラフに
のセパレータが存在するかはかなり重要な関心であり、なぜかというと、
のセパレータが存在するなら、分割統治アルゴリズムが使えるからです。うれしいことに、平面グラフは
のセパレータをもつことが知られており、
でセパレータを構築できますLipton & Tarjan。実際多くの平面グラフアルゴリズムはこのセパレータの性質によって高速性が導かれています。
木幅が
この記事ではあまり深く書くことがないです。
たぶん上級編
直線による描画
平面グラフの定義において、平面に描画するときに直線を使う必要はありませんが(曲線でよい)、実は任意の平面グラフは直線のみを用いて平面に描画が可能です。もっと言うと、のサイズのグリッド上の格子点に頂点を配置して、かつ、直線のみを使って描画することも可能です。
最大カット
最大カット問題は、一般グラフにおいてNP-Hardであることが知られていますが、平面グラフにはアルゴリズムが存在します
アルゴリズムの説明
これもまたさまざまなアルゴリズムが提案されてきたのですが、シンプルで有名なのがA simple MAX-CUT algorithm for planar graphsだと思います。
 平面グラフと双対グラフです。
平面グラフと双対グラフです。
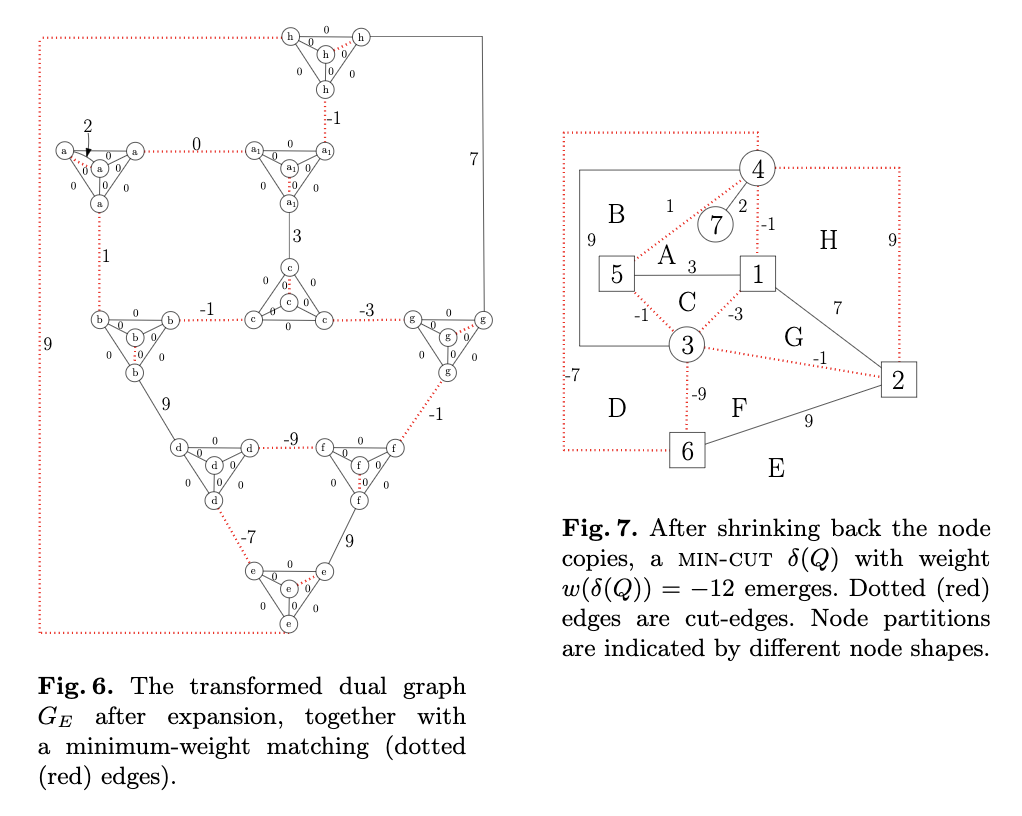 頂点を
頂点をに倍加して、最大マッチングを考えます。
連結な単純グラフ
が入力として与えられたとき、まず
の双対グラフ
をとる。双対グラフの辺のコストは、その辺が横切る元のグラフの辺のコストと同じにする。
の次数5以上の頂点を分割し、分割した頂点同士をコスト0の辺でつなぐ。さらに、
の各頂点を
に置き換えたグラフを考える。
内部の辺の重みは0.
以上のグラフでmaximum weighted matchingを考える。必ずperfect matchingが存在することが示せ、このとき、各
に着目すると必ず
から外に出る辺は偶数本になっていることがわかり、perfect matchingはEulerianになることがわかる。
双対グラフでのEulerian subgraphと元のグラフのカットには1対1対応があり、この最大重みeulerian subgraphが元のグラフでの最大cutになっている。
計算量についてまとめます。平面グラフの双対グラフも平面グラフであり、頂点数、辺の本数もで、頂点を4倍加してもオーダーは変わりません。あとは平面グラフのmaximum weighted matchingを考えればいいのですが、これはTarjanによると
なので、そのままmax-cutもこのオーダーで解けることになります(クソ雑)。
最小交差数
A separator theorem for minor-closed classesによると、固定されたについて最小交差数が
以下か判定する線形アルゴリズムがあるそうです。
同型判定
平面グラフの同型判定は線形で可能です https://dl.acm.org/citation.cfm?id=803896
Minor-closedグラフとセパレータ
さて、平面グラフはminor-closedなグラフのクラスでしたが、minor-closedな性質をもつぐらふの集合は他にもあります。たとえば、toroidalグラフとよばれる、torusに辺の交差なしに埋め込めるグラフもminor-closedです。
A Separator Theorem in Minor-Closed Classesでは、minor-closedなグラフはのセパレータをもつのでは?という話がされていて、実際に
をマイナーとして含まないグラフについて
のセパレータを持つことを証明しています。これは応用範囲が広く、たとえばbounded degreeのグラフが
のセパレータをもつことなどがすぐに導かれます。
ちなみに、bounded average degreeグラフはこの性質を満たしません(証明はErdos)。
のセパレータをもつなら、分割統治が回るので、平面グラフ以外にも多くのminor-closedなグラフについて平面グラフの場合と類似する高速なアルゴリズムがあると思います(あまり詳しくありません)
最後に
平面グラフやべーーーーー やべーーーと話題に
気になったポスター
IPのBranch&Broundを、GCNNを使って決定するという論文。なんでGCNNなのか結局ポスターを見る限りはわからなかった。比較対象がみんなアで、そんなに強くなさそう感がすごい。

joisino論文。distributed local algorithmという視点がいいし安心の解析がある。

手書きポスターニキ。ERランダムグラフから適当に辺を取り除いたグラフ同士の同型テスト(matching)やSimilarityを求める多項式アルゴリズム・準多項式アルゴリズムを作った。すげ絵

cascading portfolio problemとは、アルゴリズムとテストケースがあり、それぞれのアルゴリズムがどのテストケースをpassするかや、実行時間が分かっているときに、アルゴリズムの順序で、「テストごとの、初めてテストを通過するまでの時間、の和」を最小化するものを求める問題。いろいろなFPTを構成いている。なぜNIPSに出した。

Optimal Transportの計算量を久しぶりに改善したらしい。かなりグラフ理論系

点の追加や削除にも対応したFacility Location問題を解いているっぽい。とりあえず愚直よりよい計算量が挙げられたと書いているけど、クエリ毎はうくにきあちゃんだろ。

Universal Approximation Theorem for GNNs?
絶対に後で読む。

うわさのpaper. NNの中には構造的に特定の判定問題を得意とするものがありそうで、実際ランダムにネットワークを構築しながら探索する手法で、従来のよりもずっと小規模なネットワークで匹敵する性能のものを発見。

グラフ上のsemi-supervised learningでベンチマークを軒並み改善していそう

特徴のあるグラフについて、そのグラフラプラシアンを解析することで、analyticalに性質を検証するっぽい。

うわさの論文2. 後で読む。

グラフの特徴量をdiffuseしたらいろいろうれしいという論文だった気がする。汎用的手法っぽい。

これかなりすごい。GNNが任意のグラフを識別できることとグラフについての任意の関数を近似できることが等価であることを示したっぽい。後で読む。

よくわからんけどボロノイ図出てきたから興味ある。

タイトル的にかなり面白そう。後で読む。

タイトル的に面白そうでかなり人がいたので写真を撮った。

kNNを学習するのすごい。

ピクセルごとに微妙に加減する攻撃はあるけど、ある関数を作用させる攻撃はあんまりなさそうで、それを考案した。出力画像がなめらかなのが、見た目的な特徴っぽい。

既存のクラスタリングアルゴリズムにえいやっとすると、fairなクラスタリングがほぼ同じ精度でできるっぽい。fairとは、大きさが偏っていないということ

クラスタリングをtime seriesでやるっぽい。内容はしらんけどアイデアおもろそう。

ランダムなネットワークの入力ビットをどれほどflipすると結果が変わるか、そして学習済みモデルだとどうなるか、を調べた論文

Optimal Transportしらんけどグラフの距離を測るのはおもしろい。

上に同じく。

すごく面白い観点からGCNの性質を見ていると思う。後で読みたい。

グラフの距離おもしろい定期。

GNN関係なさすぎるけどこんなことができるのか系。普通にすごすぎる。見世物として完成度高い。

タイトル的にメモ。

上に同じ。そろそろ疲れた。

ポスターやべ〜〜〜〜〜。今度読むかも

VCのLP緩和がHalfIntである証明
https://theory.epfl.ch/osven/courses/Approx13/Notes/lecture6.pdf
LP緩和の解はシンプレックスの端点であり、シンプレックスの端点は、「異なる2つの実行可能解の合成でかけないこと」と同値。
non-halfintがあったとすると、その解をεだけ上下にずらしたものも解になることを示し、矛盾を導く。